NOI2019D2T3

交互题

首先解释交互题是什么,通俗一点,就是 出题人把答案放在了输入数据里面! 但是你不能知道实际的全部输入信息,你只能根据他给出的几个信息和调用提前实现好的函数猜出这个输入数据

这个解释可能不太对,但对这个题是有用的

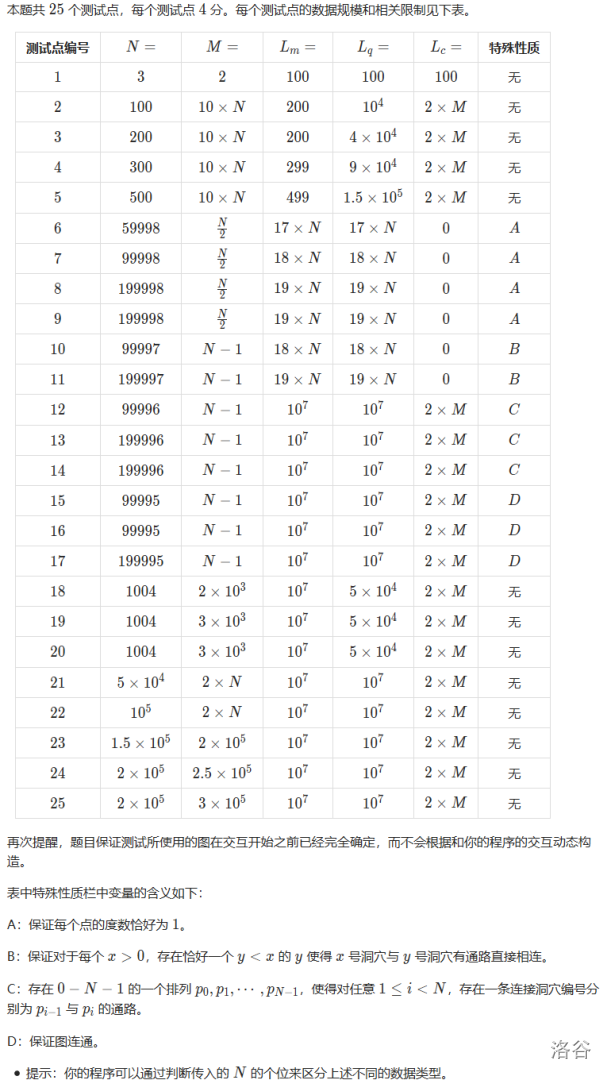
交互题不能没有这个啊

部分分1

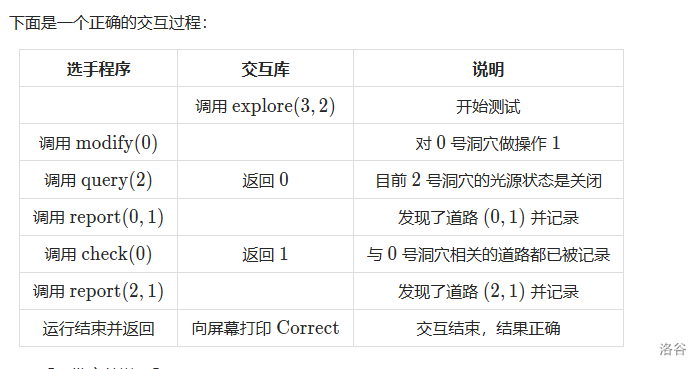
照此过程模拟即可,只要你能成功实现交互!

4pts

部分分2~5

只要有一点点暴力的想法,你会发现,如果我们想找一个点周围的边,那么只需要把这个点modify一次,然后把所有点全部query一遍,其中是亮的我们就record他们之间的一条边,再把这个点modify回去就好

然而直接这样是不行的,我们只需要稍稍优化下暴力,查询只查询和亮暗情况之前有变化的点,就可以省去最后改回来的一次,然后每次只query所有编号大于当前点的点,就可以让总查询数变成$n^2/2$,过掉第5个点

16pts

部分分 6~9

满足图由许多两个点的块组成,也就是我们要确定每个点是另外哪个点连着的

这部分也不难想,因为我们仔细观察数据范围可以得出算法的消耗应该是$nlogn$

而logn的算法...而且是交互题....比较泛用的好像有二进制啊?

做法也就同样有了,我们按照点的编号第x位二进制是1/0把所有点分成两组,然后把所有是1的点提出来点亮,然后花费n的代价查一遍全局,我们得到一个亮暗集合...那么观察不难的出

如果一个点和他的相连点这一位相同,那一定处于暗集合,这一位不同一定处于亮集合

这样我们把所有位都做一遍,再处理一下每个点就能得到每个点对应的点了!

复杂度...全都是$O(nlogn)$

16pts

部分分10~11

这一部分是最为关键的??

满足编号大的只向编号小的连一条边

乍一想和之前的做法好像没有任何关系....除了复杂度....

所以我们还是要想一个log做法?好像还有二分也是log的

那这个题我们对于一个点可以找到他二分范围和性质吗?

很容易发现:二分范围就是这个点编号到1,性质就是点亮一个前缀看他亮不亮,在某个位置之后一定全都亮

有这个性质我们就可以对于单个点二分了....而我们有n个点?整体二分就好啦

代价还是$O(nlogn)$

8pts

部分分12~14

满足图是一条链

这一部分可能比较需要灵机一动?qwq

因为做法很简单....每个点只会受到两个点的影响...如果我们先花掉O(n)的时间找到一个初始点,然后从初始点向两侧扩展...好像就满足每个点只受到一个点的影响了!因为另一个点已知,完全可以计算出那个点的影响

只受到一个点的影响?回到第三档部分分

12pts

部分分15~17

被迫营业树的部分QAQ

之前一部分已经提示我们可以通过一次次扩展点来消掉周围点异或值是一些点的异或和的做法...

那么树,他没有环,我们应该也是可以通过以这个扩展消掉异或和的

• 我们只需要求出每个点u周围点的编号的异或和,然后如果修改这个和表示的点导致u发生改变那么他们之间就有一条边

为啥正确呢?首先你会发现叶子这个性质一定成立

而非叶子我们只需要把叶子从这个树上剥离,也就是消掉他的影响,也总有一天会变成叶子就成立了

12pts

至此所有非正解做法都讲完了,其实这道NOID2T3的题对于真正NOI选手68pts都不难呢

正解

你会发现我们现在都还没有用过这个check,所以正解一定很坑

没错,正解需要一点随机化/xyx

同时,我们可能还需要一个复杂度带log的做法...如果我们把之前的两个做法融合一下,我们可以想到能不能划分出一个集合,然后在集合里整体二分呢?

这看上去完全是硬凑,但是想一下和之前的区别,之前是知道一定只有一条边在前面,所以我们一定能满足单调性

但如果我们限制一下二分的过程,然后把奇偶性作为判断的标准呢?你会发现我们一定可以对于前面是奇数条边的点连出边,而前面是偶数的由于整体二分可能判断不了有没有边,因为点亮前缀后他状态没变

所以我们直接按照这个方法去做,就可以连好某个排列里面满足前面边是奇数的那些边

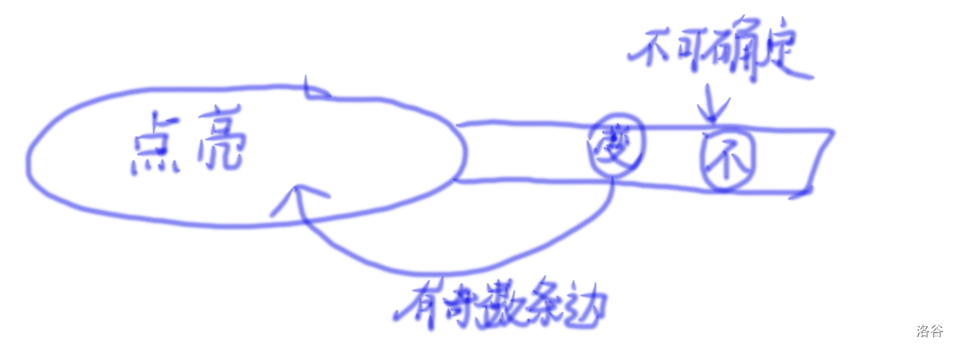
但是显然连得不够啊....所以我们只需要random_shuffle一个新的排列,然后再在这个排列上做这个事情,就又能够连出去一些边了!

其中check可以用来减少运算量的,如果一个点的周围的边都被标记了下次整体二分就不要把这个点加进去了

然后你肯定要问这样怎么保证复杂度啊

题解有一个结论:rand的一个排列里面有差不多$n/3$个点向前连边是奇数个

不会证,但这道题做完了,完结散花!!

QAQ

写的还不错吧留个赞再走呗

nmmp的洛谷不过,那为什么I君的商店有题解?